Future Modeling Road Map¶

System Design Optimization¶

The current baseline appears to be a feasible design, but the design space is large (and will grow with additional models) and needs to be more fully explored. Overall, the goal of the hyperloop design should be to find the right compromise between maximum passenger throughput, minimum travel time, and minimum cost per trip. The following are some major open questions about the hyperloop design space:

1) What is the relationship between overall energy usage and tube pressure? Would a slightly higher pressure lower the overall energy consumption by reducing vacuum pump effort more than it increases power requirements for the pod?

2) What is the best combination of pressure ratios for the compression system? Does the bypass air need to be pressurized so highly?

3) What is the best size for the tube diameter? Larger diameters will increase pump effort, but decrease pod power usage? Could a larger diameter coupled with a slightly higher pressure provide superior performance?

Geometry¶

This model makes some simple geometric calculations, however a real parametric geometry model needs to be included. This model is necessary to properly consider the layout and packaging issues involved in the design, but it also needed to do more complete structural analyses on the pressurized containers as well as to do an aerodynamic shape optimization of the outer shape.

Some alternate configurations could possibly considered as well. Although the length of the capsule would grow by a factor of almost 2, it might be possible to put the seats in a single file layout to reduce the overall tube dimensions. The effect of this change on the overall system is not obvious and needs to be studied.

The geometry model needs to be built in an open source geometry system so that it can be freely shared with the rest of the model.

Battery and Motors¶

The initial estimates of battery size and weight rely on ridiculously simple calculations. As noted, the power requirements amount to roughly 3 to 5 battery packs from a Tesla Model-S. Much better weight and size estimates for these off-the-shelf batteries need to be integrated.

No work has been done to size the motors or account for any cooling requirements they might need. Although the current results indicate that a cooling system for the compressed air is not needed, you may still need something to cool the batteries and motors. The power requirements, weight, and space needs of such cooling systems needs to be considered.

Air Bearings¶

The current models assume a fixed mass flow requirement for the air bearing system. A more accurate model would account for the overall weight of the pod, the pressure of the air, and the overall bearing size. A more detailed bearing model should be coupled to the compression system model to ensure a feasible design is achieved.

In addition, some investigations need to be made into the lower speed operation of the pod. It’s possible that splitting the compression system into two independent paths would be beneficial, if the bearings require a relatively constant mass flow rate and pressure, because it would allow a more flexible operation of what is currently the first stage compressor.

Vacuum Pumps¶

The current model indicates that a tube with around a 4 meter diameter will be needed to reach the high velocities to keep the travel time to around 35 minutes. The size of the tubes will impact to key power requirements for the vaccum pumps:

1. The peak power requirements to pump the tubes down in a reasonable time
2. The steady state power requirements to maintain the high vaccum in the tube

Both of these aspects need to be modeled and incorporated into the system models.

Solar Power Generation¶

One of the proposed features of the hyperloop concept is its near net-zero energy consumption, via the inclusion of solar panels along the length of the tubes. Models are needed to predict, based on geographical location, weather, and time of year, how much power could be produced on an ongoing basis from such a solar panel system.

The power production and power consumption of the hyperloop system need to be compared. Even assuming you can reach a net zero energy usage on an average basis, the timing of the production and consumption has a strong impact on how much energy storage is necessary in the overall system. This will have an impact on it’s overall cost.

Pod Structural Design¶

The passenger pod is, from a structural perspective, a pressure vessel experiencing a fairly pressure ratio of around 1000. The original design concept calls for a non-circular pressure vessel which raises some structural design issues. It’s possible to design an effective structure using modern aircraft grade composites technologies, but it’s possible that a round cross section could allow for a more traditional construction and reduce costs. Structural models considering composites and metallic construction are needed.

Component Mass Estimation¶

The current model does not include any significant weight estimation. Every part of the model needs to have weight estimates added.

Linear Accelerators¶

These are not considered at all currently. However, they will obviously need to be modeled as part of the mission analysis work.

Route Optimization¶

The current mission analysis takes the velocity profile in the original proposal as a given. We normalize this profile in both time and velocity, then integrate it. This gives a speed factor of about .8. So for any given maximum velocity, the average velocity would be about 80% of it.

While this simple method provides some basic dependence of travel time on overall speed and tube length it is not really sufficient. A more advanced analysis needs to be constructed which accounts for actual passenger G-load constraints and can derive an optimal route and speed profile for a given design.

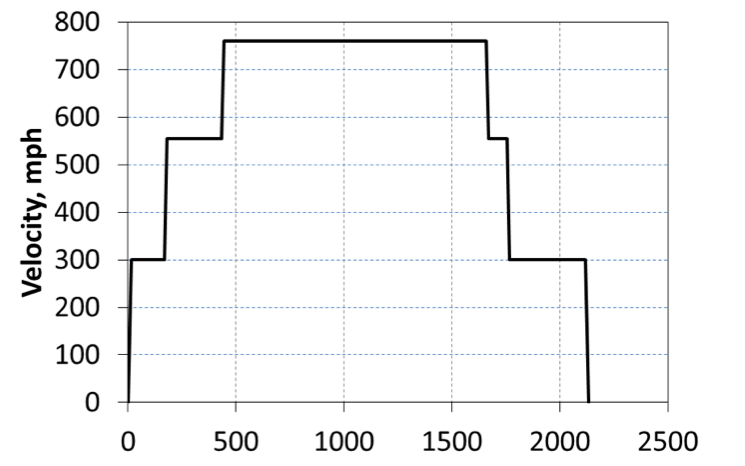
Velocity profile given in the original proposal